
Az Amerikai Matematikusok Szövetségének épületének padlója Washingtonban stílszerűen azonos, ötszög alakú csempékkel van kikövezve
A matematikai értelemben vett csempézés világában ennél nagyobb dolog nem történhet, de a hír a fürdőszoba vagy terasz csempézőknek is izgalmas lehet! A matematikus vénájú burkolókról, ill. a jó üzleti (és geometriai…) érzékkel megáldott csempegyártókról nem is beszélve!
Előrebocsátjuk, hogy ez a cikk egyszerre lesz kicsit tudományos és kicsit hétköznapi, ki-ki eldöntheti, hogy milyen szemmel olvassa, és mit ugrik át…
A sík csempézése
Ha egy vízszintes felületet átlapolódás és hézagmentesen le tudunk fedni azonos méretű és formájú alakzatokkal, akkor az az alakzat képes „csempézni a síkot”.
Ha hiszik, ha nem, ez a művelet bármely háromszöggel megtehető. Bármely – nem feltétlen szabályos – négyszög szintén képes a sík csempézésére.
A dolog az ötszögektől kezd izgalmassá válni. Egy szabályos pentagon nem alkalmas a sík csempézésére, néhány szabálytalan ötszög azonban képes erre. (Egy szabályos ötszögnek 5 azonos hosszú oldala van és minden belső szöge is egyforma, gondoljunk csak az USA Védelmi Minisztériumának emblematikus épületére, a Pentagonra, mely nem véletlenül kapta ezt a nevet, és mely egy szabályos ötszög, pentagon.)
Csempéző pentagonok felfedezése
A sík csempézésére alkalmas ötszögek megtalálása és kategorizálása majdnem egy évszázada foglalkoztatja a matematikusokat, élükön Karl Reinhardt német matematikussal, aki 1918-ban öt olyan ötszög-típust fedezett fel, mely csempézésre alkalmas. Az egyértelműség kedvéért tisztázzuk, hogy nem 5 darab ötszöget fedezett fel, hanem ötszögek 5 különböző osztályát (típusát), melyek egy-egy képlettel írhatók le. Gondoljunk csak bele, hogy ha egy adott ötszög csempézi a teret, akkor, ha ezt az ötszöget (torzítás nélkül) felnagyítjuk, az új is rendelkezni fog ugyanezzel a tulajdonsággal. További megszorítás, hogy csak konvex sokszögekről gondolkodunk, a legtöbb ember ezeket tekinti hétköznapi értelemben „sokszögnek” (tehát olyan sokszögek, melynek „a belsejében egy ember nem tud a másik elől elbújni” avagy „nincs behorpadva”).

Konvex, konkáv, ill. önmagát metsző síkidomok
A legtöbben azt gondolták, hogy Reinhardt listája teljes, mígnem fél évszázaddal később 1968-ban R. B. Kershner három további típust talált. Richard James 1975-ben még egy típust fedezett fel, ezzel 9-re növelve a felfedezett ötszög típusok számát.
Ugyanebben az évben egy váratlan résztvevő kapcsolódott be a versenybe: Marjorie Rice, egy az 50-es éveiben járó San Diego-i háziasszony, aki egy matematikai lapban olvasott James felfedezéséről. Az amatőr matematikus hölgy saját leírást és metodikát fejlesztett ki, és a következő években további négy ötszög típust fedezett fel, melyek mind-mind csempézik a síkot. 1985-ben Rolf Stein megtalálta a 14-dik típust. Megállíthatatlannak tűnt a fejlődés!
Ám innentől kezdve nem jöttek az eredmények. Egészen a múlt hónapig, amikor Casey Mann, Jennifer McLoud és David Von Derau, a University of Washington Bothell matematikusai, bejelentették, hogy egy újabb ötszög típust találtak. Az új ötszög egyszerű és nagyszerű a maga nemében, íme:
„Az új ötszög-csempét számítógéppel találtuk meg, mely kimerítő keresést végzett nagy, de nem végtelen számú lehetőség közül”, mondta Casey. „Természetesen nagyon izgatottak voltunk, és egy kicsit meg is lepődtünk, hogy egy új típust is találtunk”.
Az ötszögek tartanak számot a legnagyobb matematikai érdeklődésre csempézés szempontjából, mert ez az egyetlen sokszög típus, melyet még nem tártak fel teljes egészében.
Ahogy korábban említettük, minden háromszög és négyszög alkalmas a sík lefedésére. 1963-ban bebizonyították, hogy konvex hatszögből (hexagon) pontosan három fajta képes ugyanerre. Szintén bizonyított, hogy semmilyen hétszög, nyolcszög, vagy még több csúcsú sokszög nem alkalmas csempézésre. Ilyennel nem is érdemes próbálkozni a fürdőszobában! De az ötszögek kategorizálása továbbra is nyitott terület.

Jól ismert hatszög forma, csempeként és térkőként is találkozhatunk vele
„A síkot csempéző ötszögek osztályozása gyönyörű matematikai probléma. A feladat maga azonban olyan egyszerű, hogy egy gyermeknek is hamar elmagyarázható. Az egzakt megoldás azonban évszázadok óta húzódik ”.
Az ötszög-csempézés tanulmányozása azért is érdekes, mert gyakorlati alkalmazásai lehetnek. „Számos struktúra, melyet a természet alkotott (a kristályoktól a vírusokig), apró, szabályos építőelemekből áll össze egy nagyméretű egésszé a geometria és más fizikai erők hatására”.
„Nem szeretnék jóslásokba bocsátkozni a tekintetben, hogy találunk-e még további ötszög csempéket, de nincs olyan bizonyíték, mely kizárná ezt, és reménykedünk, hogy tényleg fogunk találni még egy párat. A számítógépes keresés futtatásának eredményeképpen reméljük, hogy hamarosan annyi adat gyűlik össze, hogy abból már releváns következtetések vonhatók le.”
Addig is az alábbi ötszög mintákból választhat az, aki ki akarja csempézni a fürdőszobája padlóját. A részletes csempézési rajzok itt találhatók. A felfogadott (vélhetően vállalkozó kedvű) mesterembernek feltétlenül adjuk ezt előzetesen oda!
Forrás:
The Guardian








.jpg)




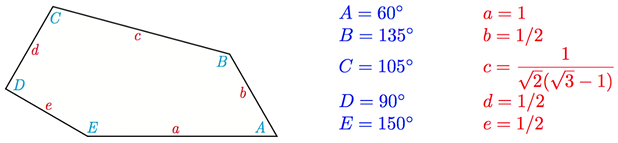


 Cikk elejére
Cikk elejére





